how to find angle of elevation

Finding an Angle in a Right Angled Triangle

Angle from Any Two Sides

We can find an unknown angle in a right-angled triangle, as long as we know the lengths of two of its sides.

ladder against wall

Example

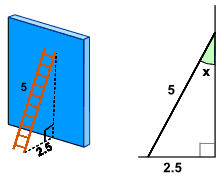
The ladder leans against a wall as shown.

What is the angle between the ladder and the wall?

The answer is to use Sine, Cosine or Tangent!

But which one to use? We have a special phrase "SOHCAHTOA" to help us, and we use it like this:

Step 1: find the names of the two sides we know

triangle showing Opposite, Adjacent and Hypotenuse

Adjacent is adjacent to the angle,
Opposite is opposite the angle,
and the longest side is the Hypotenuse.

Example: in our ladder example we know the length of:

the side Opposite the angle "x", which is 2.5
the longest side, called the Hypotenuse, which is 5

Step 2: now use the first letters of those two sides (Opposite and Hypotenuse) and the phrase "SOHCAHTOA" to find which one of Sine, Cosine or Tangent to use:

*SOH...*	Sine: sin(θ) = Opposite / Hypotenuse
*...CAH...*	Cosine: cos(θ) = Adjacent / Hypotenuse
*...TOA*	Tangent: tan(θ) = Opposite / Adjacent

In our example that is Opposite and Hypotenuse, and that gives us "SOHcahtoa", which tells us we need to use Sine.

Step 3: Put our values into the Sine equation:

Sin (x) = Opposite / Hypotenuse = 2.5 / 5 = 0.5

Step 4: Now solve that equation!

sin(x) = 0.5

Next (trust me for the moment) we can re-arrange that into this:

x = sin^-1(0.5)

And then get our calculator, key in 0.5 and use the sin^-1 button to get the answer:

x = 30°

And we have our answer!

But what is the meaning of sin^-1 … ?

Well, the Sine function "sin" takes an angle and gives us the ratio "opposite/hypotenuse",

sin vs sin-1

But sin^-1 (called "inverse sine") goes the other way ...
... it takes the ratio "opposite/hypotenuse" and gives us an angle.

Example:

Sine Function: sin(30°) = 0.5
Inverse Sine Function: sin^-1(0.5) = 30°

On the calculator press one of the following (depending
on your brand of calculator): either '2ndF sin' or 'shift sin'.

On your calculator, try using sin and sin^-1 to see what results you get!

Also try cos and cos^-1 . And tan and tan^-1 .
Go on, have a try now.

Step By Step

These are the four steps we need to follow:

Step 1 Find which two sides we know – out of Opposite, Adjacent and Hypotenuse.
Step 2 Use SOHCAHTOA to decide which one of Sine, Cosine or Tangent to use in this question.
Step 3 For Sine calculate Opposite/Hypotenuse, for Cosine calculate Adjacent/Hypotenuse or for Tangent calculate Opposite/Adjacent.
Step 4 Find the angle from your calculator, using one of sin^-1, cos^-1 or tan^-1

Examples

Let's look at a couple more examples:

trig example airplane 400, 300

Example

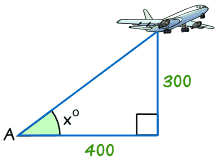
Find the angle of elevation of the plane from point A on the ground.

Step 1 The two sides we know are Opposite (300) and Adjacent (400).
Step 2 SOHCAHTOA tells us we must use Tangent.
Step 3 Calculate Opposite/Adjacent = 300/400 = 0.75
Step 4 Find the angle from your calculator using tan^-1

Tan x° = opposite/adjacent = 300/400 = 0.75

tan^-1 of 0.75 = 36.9° (correct to 1 decimal place)

Unless you're told otherwise, angles are usually rounded to one place of decimals.

trig example

Example

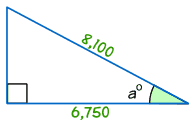
Find the size of angle a°

Step 1 The two sides we know are Adjacent (6,750) and Hypotenuse (8,100).
Step 2 SOHCAHTOA tells us we must use Cosine.
Step 3 Calculate Adjacent / Hypotenuse = 6,750/8,100 = 0.8333
Step 4 Find the angle from your calculator using cos^-1 of 0.8333:

cos a° = 6,750/8,100 = 0.8333

cos^-1 of 0.8333 = 33.6° (to 1 decimal place)

250, 1500, 1501, 1502, 251, 1503, 2349, 2350, 2351, 3934